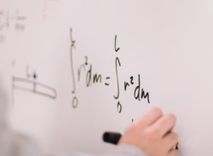
Verluste von Faktorzertifikaten

„Schließen Sie nur Finanzgeschäfte ab, die Sie vollständig verstehen“ ist ein häufiger Rat an Verbraucher. Manchmal fällt es aber auch professionellen Anlegern schwer, ein Finanzprodukt vollständig zu verstehen. Ein Beispiel ist der Verlust, den Faktorzertifikate bei Seitwärtsbewegungen des Marktes erzielen.

Ein Anleger, der ein Zertifikat kauft, verleiht damit Geld an die Bank, die das Zertifikat emittiert. Wie die Bank dieses Geld zurückzahlt und verzinst, ist dabei an zuvor vereinbarte Regeln geknüpft. Beim Aufstellen der Regeln sind der Phantasie wenig Grenzen gesetzt. So kann die Verzinsung eines Zertifikats vom Aktienkurs von BMW abhängen, dem Ölpreis oder dem EUR/USD-Wechselkurs. Anleger streben in der Regel mit dem Kauf eines Zertifikats eine höhere Verzinsung ihres Geldes als auf dem Sparbuch an. Die Vielzahl an Zertifikaten ermöglicht es den Anlegern auch, auf bestimmte Ereignisse zu spekulieren.

Ist ein Anleger davon überzeugt, dass der deutsche Aktienmarkt in naher Zukunft steigt, könnte er schlicht einen DAX-ETF – vereinfacht gesagt einen Korb deutscher Aktien, der den Aktienindex DAX nachbildet - kaufen. Durch Zertifikate könnte er diese Strategie aber auch mit einem sogenannten Hebel umsetzen. Hierdurch könnte der Anleger von einer Kursentwicklung überproportional profitieren. Mit einem Faktorzertifikat mit dem Hebel 3 würde der Anleger ein Plus von 30% erzielen, wenn der Basiswert – im Beispiel der DAX - nur um 10% steigt. Umgekehrt macht er auch einen Verlust von 60%, wenn der Basiswert um 20% fällt. Bewegt sich Faktorzertifikat in die gleiche Richtung wie der Basiswert, spricht man von einem Long-Faktorzertifikat. Bei einem Short-Zertifikat bewegt sich der Zertifikatwert hingegen entgegengesetzt, d.h. ein Short-Zertifikat mit Hebel 5 macht einen Gewinn von 50%, wenn der Basiswert um 10% sinkt. Steigt hingegen der Basiswert um 5%, macht das Short-Zertifikat einen Verlust von 25%. 

Mit Long- und Shortzertifikaten steht somit ein scheinbar einfaches Finanzprodukt zur Verfügung, mit dem gehebelt auf eine Marktentwicklung gewettet werden kann. Üblicherweise kann man nur gehebelt investieren, wenn man einen Kredit aufnimmt. Der große Vorteil eines Faktorzertifikats gegenüber der Spekulation auf Kredit ist, dass man beim Faktorzertifikat maximal seinen Einsatz verlieren kann, während bei der Spekulation auf Kredit auch höhere Verluste möglich sind. Allerdings haben die Faktorzertifikate eine recht überraschende Eigenschaft bei „Seitwärtsbewegungen“ des Marktes, ein Euphemismus dafür, dass sich der Markt gerade nicht bewegt. Tiefere Ursache ist, dass die Wertänderung des Zertifikats die tägliche relative Änderung des Basiswerts nachvollzieht. Somit schlagen sich auch die oben genannten Wertänderungen des Zertifikats so genau auch nur bei täglichen Schwankungen nieder. Steigt hingegen der DAX nicht an einem Tag um 10%, sondern innerhalb eines Monats, so steigt ein Long-Faktorzertifikat mit Hebel 5 innerhalb des Monats nicht notwendigerweise um 50%. Um wieviel das Zertifikat sich tatsächlich ändert, hängt von dem Weg ab, auf dem der Basiswert um die 10% steigt. Besonders frappierend ist dies, wenn der Basiswert irgendwann wieder sein altes Kursniveau erreicht. 

Angenommen, der Basiswert, z.B. der DAX, steigt von 100 auf 101 (1% Gewinn), um am darauf folgenden Tag wieder auf 100 (0,99% Verlust) zu fallen. Ein DAX-Anleger hätte in dieser Zeit also weder Gewinn noch Verlust gemacht. Ein Inhaber eines Faktorzertifikats verliert in dieser Zeit allerdings. Beispielsweise steigt der Kurs eines Long-Faktorzertifikats mit Hebel 5 zunächst von 100 auf 105 (5x 1%= 5% Gewinn), am darauf folgenden Tag fällt es auf 99,8 (5x0,99% = 4,95%). Ein Short-Faktorzertifikat mit Faktor 3 fällt hingegen zunächst auf 97 (3x1% = 3% Verlust), um dann auf nur 99,88 (3x0,99% = 2,97% Gewinn) zu steigen. Sowohl im Long- als auch im Short-Faktorzertifikat  erzielt man also nach zwei Tagen einen Verlust, obwohl der Basiswert wieder am Ausgangspunkt angekommen ist. Im obigen Beispiel sind die Verluste marginal. Über die Zeit können sich diese Verluste aber massiv auswirken, worauf die BaFin bereits Anfang 2020 hinwies.  (https://www.bafin.de/SharedDocs/Veroeffentlichungen/DE/Fachartikel/2020/fa_bj_2001_Faktorzertifikate.html) Die BaFin zieht hieraus den Schluss, dass die Spekulation mit Faktorzertifikaten nur für kurzfristige Anleger geeignet ist. 

Weiter unten habe ich einen mathematischen Beweis für die Verluste von Faktorzertifikaten bei Seitwärtsbewegungen eingefügt, da ich diesen in der Literatur nicht gefunden habe. Der Beweis nutzt mit der Bernoulli-Ungleichung ein jahrhundertealtes mathematisches Gesetz. Da die Bernoulli-Ungleichung auch Lernstoff von Mathematik für Wirtschaftswissenschaftler ist (http://www.math.uni-duesseldorf.de/~internet/Mathe_fuer_WiWis/WWblatt3.pdf), erscheinen mir Faktorzertifikate ein gutes Beispiel, um die Bedeutung dieser Ungleichung Studenten der Wirtschaftswissenschaften nahezubringen.

Anhang: Beweis für die Verluste von Faktorzertifikaten bei Seitwärtsbewegung des Basiswerts. 

Sofern der Basiswert nach einem beliebigen Zeitraum wieder seinen Ausgangswert erreicht, macht das Faktorzertifikat auf diesen Basiswert einen Verlust.  Diese Aussage gilt für Long- und Short-Faktorzertifikate mit ganzzahligem Faktor. Einzige Ausnahme: Bleibt der Basiswert an jedem Tag auf seinem Ausgangswert, d.h. bewegt er sich an gar keinem Tag, bleibt auch der Wert des Faktorzertifikats konstant.

Im folgenden Fall ist der 2-Perioden-Fall betrachtet. Die Verallgemeinerung auf den n-Perioden-Fall ist einfach möglich.

Seien r₁, r₂ die aufeinanderfolgenden Renditen des Basiswerts. Dieser bewege sich seitwärts, d.h. es gilt (1+r₁)(1+r₂) = 1. Damit ist r₁ > -1, r₂ > -1, d.h. es tritt kein Totalverlust des Basiswerts auf. Wir fordern zudem, dass der Hebel a ganzzahlig und mindestens 2 ist. Zudem ist 1+ar₁ > 0 und 1+ar₂ > 0 im Falle der Long-Faktorzertifikate, und 1-ar₁ > 0 und 1-ar₂ > 0, im Falle der Short.Faktorzertifikate, da andernfalls ein Totalverlust im Zertifikat auftritt und die Behauptung trivialerweise erfüllt ist. Wir wissen zudem, dass r₁ <>0 oder r₂ <>0, da wir den Fall, dass der Basiswert sich gar nicht bewegt, ausgeschlossen haben 

Für Long-Faktorzertifikate gilt: Das Zertifikat,das zu Beginn den Kurs K hat, hat nach den zwei Tagen den Kurs K(1+ar₁)(1+ar₂).  Laut der Bernoulli-Ungleichung  ist (1+ar) <= (1+r)^a für alle natürlichen Zahlen a und r größer -1. Ist r <> 0 und a > 1, gilt echte Ungleichheit. Damit ist

K(1+ar₁)(1+ar₂)< K[(1+r₁)(1+r₂)]^a = K, 

da r1 oder r2 von null verschieden sind. Somit ist die Aussage für Long-Faktorzertifikate bewiesen.

Für Short-Zertifikate mit Faktor a gilt: Der Kurs liegt nach zwei Tagen bei K(1-ar₁)(1-ar₂), und es gilt

K(1-ar₁)(1-ar₂)<K [(1-r₁)(1-r₂)]^a = K [(1-r₁)(1-r₂) (1+r₁)(1+r₂)]^a = K[(1-r₁²)(1-r₂²)]^a < K.